I. Giới thiệu
Có thể dùng bình nước để thắp nến, điều đó có thật không? Thật đấy!
Có đúng là rắn sợ realgar không? Điều đó là sai!
Hôm nay chúng ta sẽ thảo luận về:
Sự nhiễu loạn có thể cải thiện độ chính xác của phép đo, điều đó có đúng không?
Trong điều kiện bình thường, nhiễu là kẻ thù tự nhiên của phép đo. Nhiễu sẽ làm giảm độ chính xác của phép đo. Trong trường hợp nghiêm trọng, phép đo sẽ không được thực hiện bình thường. Từ quan điểm này, việc cho rằng nhiễu có thể cải thiện độ chính xác của phép đo là sai!
Tuy nhiên, liệu điều này luôn đúng? Có trường hợp nào mà nhiễu không làm giảm độ chính xác đo lường, mà ngược lại còn cải thiện nó không?
Câu trả lời là có!
2. Thỏa thuận về sự can thiệp
Dựa trên tình hình thực tế, chúng tôi đưa ra thỏa thuận sau đây về việc can thiệp:
- Tín hiệu nhiễu không chứa thành phần DC. Trong phép đo thực tế, nhiễu chủ yếu là nhiễu AC, và giả định này là hợp lý.
- So với điện áp DC đo được, biên độ nhiễu tương đối nhỏ. Điều này phù hợp với tình hình thực tế.
- Nhiễu là một tín hiệu tuần hoàn, hay giá trị trung bình bằng 0 trong một khoảng thời gian cố định. Điều này không nhất thiết đúng trong thực tế đo lường. Tuy nhiên, vì nhiễu thường là tín hiệu AC có tần số cao hơn, nên đối với hầu hết các loại nhiễu, quy ước giá trị trung bình bằng 0 là hợp lý trong một khoảng thời gian dài hơn.
3. Độ chính xác đo lường dưới tác động của nhiễu
Hầu hết các thiết bị đo và đồng hồ điện hiện nay đều sử dụng bộ chuyển đổi AD, và độ chính xác đo của chúng có liên quan mật thiết đến độ phân giải của bộ chuyển đổi AD. Nói chung, bộ chuyển đổi AD có độ phân giải cao hơn sẽ có độ chính xác đo cao hơn.
Tuy nhiên, độ phân giải của AD luôn bị giới hạn. Giả sử độ phân giải của AD là 3 bit và điện áp đo cao nhất là 8V, bộ chuyển đổi AD tương đương với một thang đo chia thành 8 vạch, mỗi vạch là 1V. Kết quả đo của AD này luôn là một số nguyên, và phần thập phân luôn được nhớ hoặc bỏ qua, trong bài viết này chúng ta giả định là có nhớ. Việc nhớ hoặc bỏ qua sẽ gây ra sai số đo. Ví dụ, 6,3V lớn hơn 6V và nhỏ hơn 7V. Kết quả đo của AD là 7V, và có sai số 0,7V. Chúng ta gọi sai số này là sai số lượng tử hóa của AD.
Để thuận tiện cho việc phân tích, chúng tôi giả định rằng thang đo (bộ chuyển đổi AD) không có sai số đo lường nào khác ngoài sai số lượng tử hóa AD.
Bây giờ, chúng ta sử dụng hai thang đo giống hệt nhau như vậy để đo hai điện áp DC được hiển thị trong Hình 1 mà không có nhiễu (tình huống lý tưởng) và có nhiễu.
Như thể hiện trong Hình 1, điện áp DC đo được thực tế là 6,3V, và điện áp DC trong hình bên trái không bị nhiễu, có giá trị không đổi. Hình bên phải cho thấy dòng điện một chiều bị nhiễu bởi dòng điện xoay chiều, và có sự dao động nhất định về giá trị. Điện áp DC trong sơ đồ bên phải bằng với điện áp DC trong sơ đồ bên trái sau khi loại bỏ tín hiệu nhiễu. Hình vuông màu đỏ trong hình biểu thị kết quả chuyển đổi của bộ chuyển đổi AD.

Điện áp DC lý tưởng không bị nhiễu
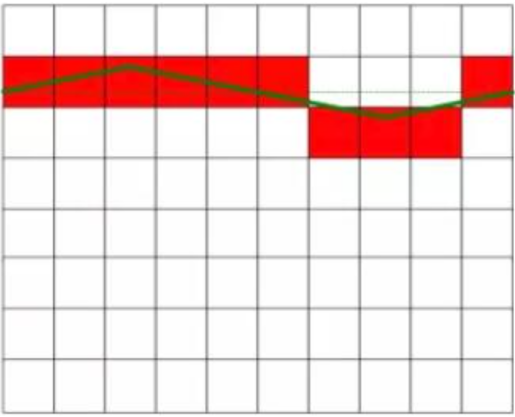
Áp dụng điện áp DC gây nhiễu có giá trị trung bình bằng không.
Thực hiện 10 phép đo dòng điện một chiều trong hai trường hợp ở hình trên, sau đó lấy giá trị trung bình của 10 phép đo đó.
Thang đo đầu tiên bên trái được đo 10 lần, và kết quả mỗi lần đều giống nhau. Do ảnh hưởng của sai số lượng tử hóa AD, mỗi lần đo đều cho kết quả 7V. Sau khi lấy trung bình 10 lần đo, kết quả vẫn là 7V. Sai số lượng tử hóa AD là 0,7V, và sai số đo cũng là 0,7V.
Thang đo thứ hai bên phải đã thay đổi đáng kể:
Do sự khác biệt về điện áp nhiễu dương và âm cũng như biên độ, sai số lượng tử hóa AD khác nhau tại các điểm đo khác nhau. Dưới sự thay đổi của sai số lượng tử hóa AD, kết quả đo AD thay đổi trong khoảng từ 6V đến 7V. Bảy trong số các phép đo cho kết quả 7V, chỉ có ba phép đo cho kết quả 6V, và trung bình của 10 phép đo là 6,3V! Sai số là 0V!
Trên thực tế, không có sai sót nào là không thể xảy ra, bởi vì trong thế giới khách quan, không có mức điện áp 6.3V tuyệt đối nào cả! Tuy nhiên, thực tế là vẫn có những sai sót như sau:
Trong trường hợp không có nhiễu, vì mỗi kết quả đo đều như nhau, nên sau khi lấy trung bình 10 lần đo, sai số vẫn không thay đổi!
Khi có lượng nhiễu thích hợp, sau khi lấy trung bình 10 phép đo, sai số lượng tử hóa AD giảm đi một bậc độ lớn! Độ phân giải được cải thiện một bậc độ lớn! Độ chính xác của phép đo cũng được cải thiện một bậc độ lớn!
Các câu hỏi then chốt là:
Hiện tượng này có giống nhau khi điện áp đo được có các giá trị khác không?
Độc giả có thể muốn tuân theo thỏa thuận về nhiễu trong phần thứ hai, biểu diễn nhiễu bằng một loạt các giá trị số, chồng nhiễu lên điện áp đo được, sau đó tính toán kết quả đo của từng điểm theo nguyên tắc truyền của bộ chuyển đổi AD, rồi tính giá trị trung bình để kiểm chứng, miễn là biên độ nhiễu có thể làm thay đổi giá trị đọc sau khi lượng tử hóa AD, và tần số lấy mẫu đủ cao (sự thay đổi biên độ nhiễu có quá trình chuyển tiếp, chứ không phải hai giá trị dương và âm), thì độ chính xác phải được cải thiện!
Có thể chứng minh rằng, miễn là điện áp đo được không phải là số nguyên chính xác (điều này không tồn tại trong thế giới khách quan), thì sẽ có sai số lượng tử hóa AD. Cho dù sai số lượng tử hóa AD lớn đến đâu, miễn là biên độ nhiễu lớn hơn sai số lượng tử hóa AD hoặc lớn hơn độ phân giải tối thiểu của AD, nó sẽ khiến kết quả đo thay đổi giữa hai giá trị liền kề. Vì nhiễu có tính đối xứng dương và âm, nên biên độ và xác suất giảm và tăng là bằng nhau. Do đó, khi giá trị thực tế gần với giá trị nào hơn, xác suất xuất hiện của giá trị nào sẽ lớn hơn, và nó sẽ gần với giá trị nào sau khi lấy trung bình.
Tức là: giá trị trung bình của nhiều phép đo (giá trị trung bình nhiễu bằng 0) phải gần hơn với kết quả đo không có nhiễu, nghĩa là, sử dụng tín hiệu nhiễu AC có giá trị trung bình bằng 0 và lấy trung bình nhiều phép đo có thể giảm sai số lượng tử hóa AD tương đương, cải thiện độ phân giải phép đo AD và nâng cao độ chính xác phép đo!
Thời gian đăng bài: 13/07/2023




